注文を終え、あとは届くのを待つだけとなったわけだが、一つ頭に疑問が思い浮かんだ。「バックアップ間隔はどれぐらいにしようか」。心配性ならば毎日バックアップを取ればよい。しかし一度のバックアップにかかる時間は数時間。毎日これをやるのは事実上ムリがある。第一余計な負荷をかけてしまい、かえってハードディスクそのものの寿命が短くなるかもしれない。

しかし間隔が長すぎると、万一ハードディスクが不具合を起こした際にデータを元に戻す過程で、「巻き戻り」「失うデータ」の量が多すぎる。いざバックアップしてあったデータを吸い出してみたら、最後にセーブしたのが一年前、という事態になれば、一年間の作業はほとんど水泡に帰してしまう。

「どのくらいの間隔でバックアップすればいいのか……」色々調べたり手持ちの資料を探ったところ、どうにか一つ、計算式による最適時間が導き出せるものを見つけた。そこでここでは、当方自身が納得・理解しやすいようかみ砕いたうえで、解説してみることにする。

●前提の設定その1

次のような前提を設定する。

この前提で、最適なバックアップの間隔x秒を求めることにする。この際、時間の経過と共に保存されているファイル数などの変化でa、bは変化しうるが、ここでは無視する。

少なくともバックアップの時間以上は間隔を採る必要があるから「a＜x」(そうでないと作業よりバックアップの時間の方が長いというお莫迦な話になる)、データ破損までにバックアップを取っておかないと意味がないので「x＜b」という、二つの不等式が必要になる。

つまり

という条件のもと、最適なバックアップ時間x秒を求めればよい。このx秒が長すぎると(バックアップ間隔が長すぎると)、データが壊れた時の巻き戻りが大きすぎて作業が進まない。かといってx秒が短い、つまり頻度が高すぎるとバックアップにばかり時間を採られてしまい、肝心の作業工程に時間を費やせなくなる。

●前提の設定その2

上記設定から、次の想定をさらに考える。

最終的にパソコン(内のハードディスク)を使い終えて新しい端末に変えるまで、t秒間そのパソコン(ハードディスク)を使うことにすると、求めるべきx秒を元に考えれば「t／x回」のバックアップが行われる。一度のバックアップに必要な時間はa秒。よって、バックアップにかかる時間は総計で「at／x秒」となる。そしてその間、作業工程は進まないから(バックアップ中にそのパソコンで作業をするのはトラブルの元)、総計でバックアップによって「ant／x工程」作業が進まないことになる。

一方、t秒間には「t／b回」データが破損してしまう計算になる。もしデータが壊れたら、直前のバックアップデータを吸い出して作業を再開しなければならない。

バックアップの繰り返しの中でどのタイミングでデータが壊れるかは未知数だが(例えば明日バックアップするつもりだったのに壊れた、という運の悪い場合もあるし、バックアップ直後に壊れたという不幸中の幸いもあるだろう)、それぞれの発生確率は均等なので、平均的にバックアップ間隔のx秒の中間と仮定する。この場合、「x／2秒」分の作業がムダになる(直前のバックアップデータと直前までやっていた作業との差)から、作業工程としては「nx／2工程」分がムダになってしまう。一度のデータ破損でムダになる工程数がこれだ。

つまり「t／b回」×「nx／2工程」で、パソコンを使い終えるまでにデータ破損でムダになる作業工程は「ntx／2b工程」となる。

●一つのパソコンを使い切るまでにこなせる作業工程は……

もし仮に一度もデータ破損がなければ、パソコンを使いきるt秒間に進めた工程は「nt工程」。バックアップに必要なのは「ant／x工程」。データ破損でムダになる作業工程は「ntx／2b工程」。これらをあわせて、上記の設定・仮定で進められる作業工程は

となる。求めたいのは「最適なバックアップ時間x秒」。つまり上記の式で最大値が出るような「x」を求めればよい。これにはxで微分して(つまりxを変数とするグラフの変動率を調べて)、その値が0となる(もっとも工程が多くなるポイント。グラフ上の頂点)値を計算すればよいことになる。

●作業工程の最大化を求めれば良い

この答えは(微分するとant／x^2－nt／2b。これイコール0となるxを方程式で求めればOK。つまりx^2＝2abとなるから)x=√2abの時。

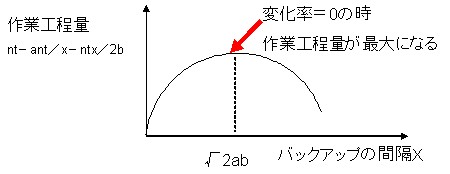
微分方程式による作業工程の最大化を求めるための概念グラフ……これを調べるために高校時代の教科書を引っ張り出してしまった(笑)

よって、バックアップ間隔は「√2ab」秒、「バックアップにかかる時間」と「平均的なデータ破損までの時間」をかけてさらに2をかけ、出てきた値をルート計算すれば良いことになる。

例えばあるハードディスクが3か月に一度止まり、バックアップには30分かかるとする。すると、

となり、約2日に一度バックアップをとればよいことになる。……案外短いのが分かる。

---

実際には複数の媒体を利用したり、差分ファイル形式(前回のバックアップファイルと比較し、変更された部分だけを差し替える)を用いることで手間や時間は随分と軽減することができる。

また、係数の一つ「平均的なデータ破損までの時間」も、よほど下手なものをつかまされない限り、「平均的」には数年単位と見てよいだろう。ただ同時に、マーフィーの法則ではないが「おきうるものは必ずおきる」可能性がある。その時が来て慌てふためくことのないよう、こまめにバックアップをとっておくにこしたことはない。

もちろん、バックアップ用のメディアを用意していないなど問題外。すぐにでも用意すべし。外付けハードディスクでなくとも、CD-RでもDVD-Rでもストレージでも良い。「その時」が来たとき、泣きを見るのは自分自身なのだから。

(最終更新:2013/09/11)