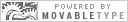「かごの卵」とリスク分散
2006年06月18日 18:00
 投資が語られる際によくたとえ話としてあげられるのが「かごと卵」の話。要は「卵を運ぶときに一つのかごにまとめて入れてしまうと、そのかごをひっくり返してしまった場合すべての卵が割れてしまう。だから卵は複数のかごに入れて運ぶべきだ」という例をあげ、リスク回避のためには分散して投資することをうながしている。この考え方についてちょっと考えてみた。
投資が語られる際によくたとえ話としてあげられるのが「かごと卵」の話。要は「卵を運ぶときに一つのかごにまとめて入れてしまうと、そのかごをひっくり返してしまった場合すべての卵が割れてしまう。だから卵は複数のかごに入れて運ぶべきだ」という例をあげ、リスク回避のためには分散して投資することをうながしている。この考え方についてちょっと考えてみた。
スポンサードリンク
分かりやすくするために「かごは1つか2つ」「卵は2つ」「中に卵がいくつ入っていようとも、1つのかごで卵を運ぶ際に途中でかごを落として中の卵を割ってしまう確率は50%」「かごを落とすと中の卵はすべて割れる」と単純化する。期待値計算をすると、かご1つの場合(パターンA)は「無事に運べる=2(A1)」か「途中でかごを落として割ってしまう=0(A2)」の二つの場合が考えられ、(2+0)÷2で1.0。平均1個のたまごを運べることになる。
一方、かご2つに1つずつ卵を分散して入れて運ぶ場合(パターンB)、それぞれのかごを落とすかどうかは互いに影響を及ぼさず独立した確率になるから、それぞれ0.5ずつの期待値(落とすか落とさないかはそれぞれ半分の確率)となり、それがかご2つ分だから0.5+0.5=1.0。なんだ同じじゃん、と思う人も多いだろう。
かごを1つにしても2つにしても期待値は同じ……?
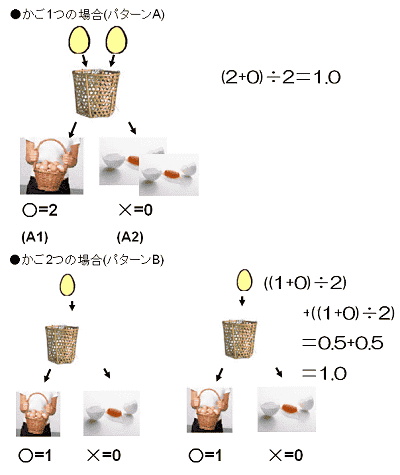
だが少し待って欲しい。期待値計算としては0.5はありうるわけだが、実際に1つのかごの中に卵が0.5個入って運び終えるという状況はありえない。後者(かご2つ、パターンB)の場合、運べたかどうかについては次の4パターン(B1、B2、B3、B4)が考えられる。すなわち1つ目のかごと2つ目のかごそれぞれについて「成功・成功」「成功・失敗」「失敗・成功」「失敗・失敗」というわけだ。これでも期待値計算上は、4パターンが同じ確率で発生しうるわけで、それぞれ結果は2、1、1、0個だから(2+1+1+0)÷4=1.0。やはり同じ。「かごを分散してもリスク分散にはならない」という結果になる。
かごを2つにした場合の可能性について詳細を考察してみる
さらにここで深く突っ込んでみることしよう。パターンA(かご1つ)とパターンB(かご2つ)それぞれについて、どんな結果が起きうるのかその可能性と共に検証してみる。すると次のようになる。
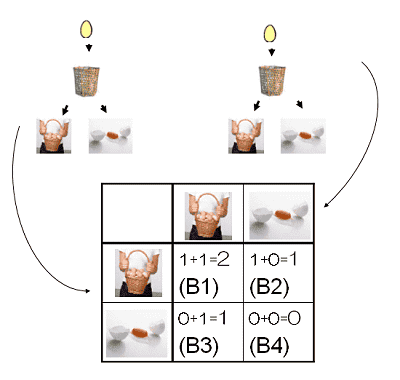
①かご1つ:(パターンA)
2つとも無事:50%(A1)
2つとも割れる:50%(A2)
②かご2つ:(パターンB)
2つとも無事:25%(B1)
1つだけ無事:50%(B2とB3)
2つとも割れる:25%(B4)
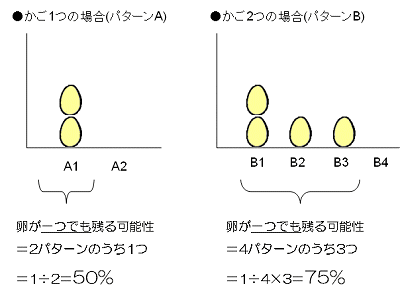
お分かりだろうか。かご2つ(パターンB)の場合、数はともかく「卵が一つでも運べる」結果はB1だけでなくB2とB3も(一つだけではあるが)含まれる。よって、「一つでもよいから卵を運ぶ」というミッションの場合は、(二つとも運べばそれに越したことはないが一つでもミッションクリアになるから)、パターンAの場合は50%に過ぎないのに対し、パターンBの場合は25%(2つとも運べる)+50%(1つだけ運べる)=75%にまで確率が跳ね上がるのだ。
かごを2つに分けた場合「卵を全滅させない可能性」は75%になる
投資における「かごの卵」を例に挙げた危険分散・リスク軽減の教えもこれに他ならない。つまり複数銘柄に投資することにより、少なくとも「大損ぶっこく」、もとい「大きなダメージを受けて」市場から退場することなく、生き残れる(卵を割らずに運び切る)可能性が高まるのである。
もちろんかごの数を増やすことで、さらなるリスク分散を図ることも可能だ。その一方、分散しすぎると管理が煩雑になるし手間も増えるので、現実的ではない。
また、発想を逆転すれば「かごの卵理論によるリスク分散」は大儲けする可能性を減らすことでもある。上の図表を例にあげれば、「2つとも卵が無事」つまり大儲けする可能性はかご1つ(パターンA)の場合50%なのに対し、かご2つ(パターンB)の場合は25%になってしまう。生き残る可能性が大きいことは、それだけ大勝利の可能性を低めてることに他ならない。図表・ビジュアル的な考え方をすれば、「成功の度合いを均(なら)して大失敗の可能性を減らす」もっと端的に表現すれば「高い山を削って谷の一部を埋める」ようなものだ。
それぞれの投資スタンスや運用資金によって、リスクの採り方やどの程度の成功を求めるのかについて、目指すところは異なる。かごを一つしか持たずに一発勝負に出るのか、いくつもかごを持って何度も行き来してみるのか、数個のかごでトライしてみるのか。それは自分の能力や考え方、そして卵の個数や周囲の状況から判断し、決めるべきだろう。
スポンサードリンク
ツイート


 最新情報をRSSで購読する
最新情報をRSSで購読する